Properties of derivative

Functions: f, g, y, u, v

Argument (independent variable): x

Real constant: k

Angle: α

1. Derivative of a function:

The derivative of a function y=f(x) measures the rate of change of y with respect to x. Suppose that at some point x ∈ R, the argument of a continuous real function y=f(x) has an increment Δx . Then the increment of the function is equal to Δy = f(x+Δx)− f(x).

The derivative of a function y=f(x) at the point x is defined as the limit of the ratio

$$ \frac { \Delta {y}}{ \Delta {x}} \ as \ \Delta {x} \rightarrow 0: $$

$$ y'=f'(x) = \frac {dy}{dx} =\frac {df(x)}{dx} $$

$$ = \lim_{x\to 0} { \frac { \Delta {y}}{ \Delta {x}}} = \lim_{x\to 0} { \frac { f(x + \Delta {x}) - f(x)}{ \Delta {x}}} $$

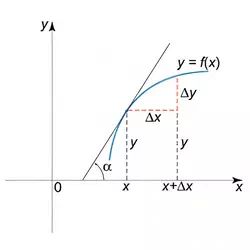
From a geometrical point of view, the derivative of a function y=f(x) at the point x is equal to the slope of the tangent line to the curve f(x) drawn through this point:

$$ \frac {dy}{dx} = \tan \alpha $$

2. Derivative of the sum of two functions:

The derivative of the sum of two functions is equal to the sum of their derivatives:

$$ \frac {d(u+v)}{dx} = \frac {du}{dx} + \frac {dv}{dx} $$

3. Derivative of the difference of two functions:

The derivative of the difference of two functions is equal to the difference of their derivatives:

$$ \frac {d(u-v)}{dx} = \frac {du}{dx} - \frac {dv}{dx} $$

4. Constant factor:

A constant factor can be taken out of a derivative:

$$ \frac {d(ku)}{dx} = k \frac {du}{dx} $$

5. Derivative of the product of two functions:

$$ \frac {d(u \cdot v)}{dx} = \frac {du}{dx} \cdot v + u \cdot \frac {dv}{dx} $$

6. Derivative of the quotient of two functions:

$$ \frac {d}{dx} \left( \frac uv \right)= \frac {\frac {du}{dx} \cdot v - u \cdot \frac {dv}{dx}}{v^2} $$

7. Derivative of a composite function (chain rule)

$$ y= f(g(x)), u=g(x), \frac {dy}{dx} = \frac {dy}{du} \cdot \frac {du}{dx} $$

8. Derivative of an inverse function:

$$ \frac {dy}{dx} = \frac {1}{dx/dy} $$

Where, x(y) is the inverse function for y(x)

$$ 9. \ \frac {d}{dx} \left( \frac 1y \right) = - \frac {dy/dx}{y^2} $$

10. Logarithmic derivative:

$$ y=f(x), \ \ln y = \ln f(x),$$

$$ \frac {dy}{dx} = f(x) \cdot \frac {d}{dx} [ \ln f(x)] $$