Parallelogram

A parallelogram is a special type of quadrilateral that has equal and parallel opposite sides.

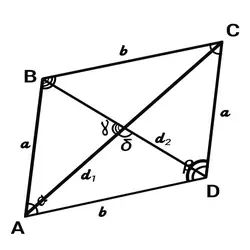
The perimeter of a parallelogram:

1. Formula of parallelogram perimeter in terms of sides:

$$ P = 2a + 2b = 2(a + b) $$

2. Formula of parallelogram perimeter in terms of one side and diagonals:

$$ P = 2a + \sqrt {2d_1^2 + 2d_2^2 - 4a^2} $$

$$ P = 2b + \sqrt {2d_1^2 + 2d_2^2 - 4b^2} $$

3. Formula of parallelogram perimeter in terms of side, height and sine of an angle:

$$ P=2 \left( b+ \frac {h_b}{\sin \alpha} \right) $$

$$ P=2 \left( a+ \frac {h_a}{\sin \alpha} \right) $$

The area of a parallelogram

1. Formula of parallelogram area in terms of side and height:

$$ A= a \cdot h_a $$

$$ A= b \cdot h_b $$

2. Formula of parallelogram area in terms of sides and sine of an angle between this sides:

$$ A = ab \sin \alpha $$

$$ A = ab \sin \beta $$

3. Formula of parallelogram area in terms of diagonals and sine of an angle between diagonals:

$$ A = \frac 12 d_1d_2 \sin \gamma $$

$$ A = \frac 12 d_1d_2 \sin \delta $$

Diagonal of a parallelogram:

1. Formula of parallelogram diagonal in terms of sides and cosine β (cosine theorem)

$$ d_1 = \sqrt {a^2 + b^2 - 2ab\cdot \cos \beta} $$

$$ d_2 = \sqrt {a^2 + b^2 + 2ab\cdot \cos \beta} $$

2. Formula of parallelogram diagonal in terms of sides and cosine α (cosine theorem)

$$ d_1 = \sqrt {a^2 + b^2 + 2ab\cdot \cos \alpha} $$

$$ d_2 = \sqrt {a^2 + b^2 - 2ab\cdot \cos \alpha} $$

3. Formula of parallelogram diagonal in terms of two sides and other diagonal:

$$ d_1 = \sqrt {2a^2 + 2b^2 - d_2^2 }$$

$$ d_2 = \sqrt {2a^2 + 2b^2 - d_1^2 }$$

4. Formula of parallelogram diagonal in terms of area, other diagonal and angles between diagonals:

$$ d_1 = \frac {2A}{d_2\cdot \sin \gamma}= \frac {2A}{d_2\cdot \sin \delta} $$

$$ d_2 = \frac {2A}{d_1\cdot \sin \gamma}= \frac {2A}{d_1\cdot \sin \delta} $$

Characterizations of a parallelogram:

Quadrilateral ABCD is a parallelogram, if at least one of the following conditions:

AB||CD, BC||AD

AB||CD, AB = CD (или BC||AD, BC = AD)

AB = CD, BC = AD

∠DAB = ∠BCD, ∠ABC = ∠CDA

AO = OC, BO = OD

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AC² + BD² = AB² + BC² + CD² + AD²

• Quadrilateral has two pairs of parallel sides:
• Quadrilateral has a pair of parallel sides with equal lengths:
• Opposite sides are equal in the quadrilateral:
• Opposite angles are equal in the quadrilateral:
• Diagonals bisect the intersection point in the quadrilateral:
• The sum of the quadrilateral angles adjacent to any side is 180°:
• The sum of the diagonals squares equals the sum of the sides squares in the quadrilateral:

The basic properties of a parallelogram:

AB = CD, BC = AD

AB||CD, BC||AD

∠ABC = ∠CDA, ∠BCD = ∠DAB

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

AO = CO = d₁/2

BO = DO = d₂/2

AC² + BD² = 2AB² + 2BC²

• Opposite sides of a parallelogram have the same length:
• Opposite sides of a parallelogram are parallel:
• Opposite angles of a parallelogram are equal:
• Sum of the parallelogram angles is equal to 360°:
• The sum of the parallelogram angles adjacent to any sides is 180°:
• Each diagonal divides the parallelogram into two equal triangle
• Two diagonals is divided parallelogram into two pairs of equal triangles
• The diagonals of a parallelogram intersect and intersection point separating each one in half:
• Intersection point of the diagonals is called a center of parallelogram symmetry
• Sum of the diagonals squares equals the sum of sides squares in parallelogram:
• Bisectors of parallelogram opposite angles are always parallel
• Bisectors of parallelogram adjacent angles always intersect at right angles (90°)