Frustum or right Circular cone

Frustum of a right circular cone is that portion of right circular cone included between the base and a section parallel to the base not passing through the vertex.

Properties of Frustum of Right Circular Cone:

• The altitude of a frustum of a right circular cone is the perpendicular distance between the two bases. It is denoted by h.
• All elements of a frustum of a right circular cone are equal. It is denoted by L.

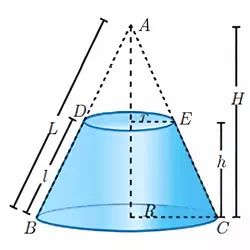
Curved surface area of a frustum :

C.S.A. of a frustum = π(R + r)l sq. units

Where,\( l=\sqrt {h^2 + (R-r)^2} \)

Example:

The slant height of a frustum of a cone is 5 cm and the radii of its ends are 4 cm and 1 cm. Find its curved surface area.

Solution:

Given that, l= 5 cm, R = 4 cm, r = 1 cm

Now, C.S.A. of the frustum = π (R + r) l sq. units

$$ = \frac {22}{7} \times (4+1) \times 5 $$

$$ = \frac {550}{7} $$

Therefore, C.S.A. = 78.57 cm²

Total surface area of a frustum:

T.S.A. of a frustum = π(R + r)l + πR² + πr ² sq. units

Where, \( l=\sqrt {h^2 + (R-r)^2} \)

Example:

An industrial metallic bucket is in the shape of the frustum of a right circular cone whose top and bottom diameters are 10 m and 4 m and whose height is 4 m. Find the total surface area of the bucket.

Solution:

Given that, diameter of the top =10 m; radius of the top R = 5 m.

diameter of the bottom = 4 m; radius of the bottom r = 2 m, height h= 4 m

$$ l=\sqrt {h^2 + (R-r)^2} $$

$$ l=\sqrt {4^2 + (5-2)^2} $$

$$ l=\sqrt {16+9} = \sqrt {25} $$

$$ l=5 \ m $$

$$ \text{T.S.A} = \pi (R + r)l + \pi R^2 + \pi r^2 $$

$$ = \frac {22}{7} [(5+2)5+25+4] $$

$$ = \frac {1408}{7} $$

$$ = 201.14 $$

T.S.A. = 201.14 m²

Volume of a frustum:

V = (πh/3)(R²+Rr+r²)

Example:

Find the volume of a frustum of a right circular cone with height 20, lower base radius 34 and top radius 19.

Solution:

Given.

h = 20, R = 34, r = 19

V =( (π×20)/3)(34²+34×19+19²)

V = 14420 π cubic units