Ellipse

In analytic geometry, an ellipse is a mathematical equation that, when graphed, resembles an egg. An ellipse has two focal points. The distance apart between the two points is one way of describing a particular ellipse. If the two points come together the ellipses become a circle with the point at its center.

Ellipse with center at the origin

Ellipse with center at the origin and major axis on the x-axis.

$$ \frac {x^2}{a^2} + \frac {y^2}{b^2} = 1 $$

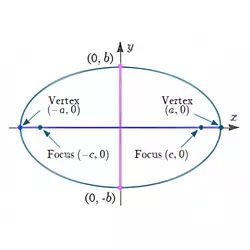
Ellipse with center at the origin and major axis on the y-axis.

$$ \frac {x^2}{b^2} + \frac {y^2}{a^2} = 1 $$

Ellipse with center at (h, k):

Ellipse with center at (h, k) and major axis parallel to the x-axis.

$$ \frac {(x-h)^2}{a^2} + \frac {(y-k)^2}{b^2} = 1 $$

Ellipse with center at (h, k) and major axis parallel to the y-axis.

$$ \frac {(x-h)^2}{b^2} + \frac {(y-k)^2}{a^2} = 1 $$

Example:

What is the standard form equation of the ellipse that has vertices (±8,0) and foci (±5,0)?

The foci are on the x-axis, so the major axis is the x-axis. Thus, the equation will have the form

$$ \frac {x^2}{a^2} + \frac {y^2}{b^2} = 1 $$

The vertices are (±8,0), so a=8 and a²=64

The foci are (±5,0), so c=5 and c²=25

We know that the vertices and foci are related by the equation c²=a²-b². solving for b², we have:

$$ 25=64-b^2 $$

$$ b^2=39 $$

The equation of the ellipse is

$$ \frac {x^2}{64} + \frac {y^2}{39} = 1 $$

Elements of Hyperbola:

Center:

The center of the ellipse has coordinates (h,k).

Major Axis:

The major axis of the ellipse is the longest width across it. For a horizontal ellipse, that axis is parallel to the x-axis. The major axis has length 2a. Its endpoints are the major axis vertices, with coordinates (h±a,k).

Minor Axis:

The minor axis of the ellipse is the shortest width across it. For a horizontal ellipse, it is parallel to the y-axis. The minor axis has length 2b. Its endpoints are the minor axis vertices, with coordinates (h,k±b).

Foci:

The foci are two points inside the ellipse that characterize its shape and curvature. For a horizontal ellipse, the foci have coordinates (h±c,k), where the focal length c is given by

$$ c^2=a^2-b^2 $$

Eccentricity:

All conic sections have an eccentricity value, denoted e. All ellipses have eccentricities in the range 0≤e<1. An eccentricity of zero is the special case where the ellipse becomes a circle. An eccentricity of 1 is a parabola, not an ellipse.

The eccentricity is defined as:

$$ e= \frac ca $$

Example:

Find the coordinates of the vertices and foci of 25x²+y²=25

$$ x^2 + \frac {y^2}{25} =1 $$

So b=1 and a=5. In this example, the major axis is vertical.

So the vertices are at (0,-5) and (0,5).

To find c, we proceed as before:

$$ c= \sqrt {a^2-b^2} $$

$$ = \sqrt {25-1} $$

$$ = \sqrt {24} $$

$$ c= 4.899 $$

So the foci are at (0,-4.9) and (0,4.9).