
Double integration

Functions of two variables: f(x,y), f(u,v), g(x,y)
Independent variables: x, y, u, v
Small changes: Δxi, Δyi
Regions of integration: R, S
Real numbers: a, b, c, d, α, β
Polar coordinates: r, θ
Area of a region: A
Surface area: S
Volume of a solid: V
Mass of a lamina: m
Density of a lamina: ρ(x,y)
First moments: Mx, My
Moments of inertia: Ix, Iy, I0
Charge of a plate: Q
Charge density: σ(x,y)
Coordinates of the center of mass: \(\bar x\), \(\bar y\)
Average of a function: μ
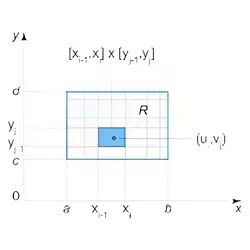
1. The double integral of a function f(x,y) over a rectangular region [a,b]×[c,d] is defined as the limit of the integral sum (Riemann sum):
$$ \iint \limits_{[a,b]×[c,d]} f(x,y) \ dA= \lim_{\substack{\text{max} \ \Delta {x_i} \to 0 \\ \text{max} \ \Delta {y_j} \to 0 }} \sum_{i=1}^m \sum_{j=1}^n f(u_i,v_j) \Delta x_i \Delta y_j, $$
where (ui,vj) is some point in the rectangle (xi−1,xi)×(yj−1,yj) and Δxi=xi−xi−1, Δyj=yj−yj−1.
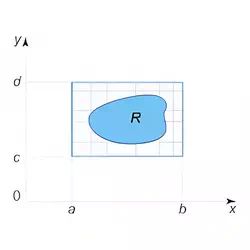
2. The double integral of a function f(x,y) over a general region R is defined to be
$$ \iint \limits_R f(x,y) \ dA= \iint \limits_{[a,b]×[c,d]} g(x,y) \ dA $$
where the rectangle [a,b]×[c,d] contains the region R. The function g(x,y) is defined as follows
g(x,y)=f(x,y) when f(x,y) is in R and g(x,y)=0 otherwise.
3. The double integral of the sum of two functions is equal to the sum of the integrals of these functions
$$ \iint \limits_R [f(x,y)+g(x,y)] \ dA = \iint \limits_R f(x,y) \ dA + \iint \limits_R g(x,y) \ dA $$
4. The double integral of the difference of two functions is equal to the difference of the integrals of these functions:
$$ \iint \limits_R [f(x,y)-g(x,y)] \ dA = \iint \limits_R f(x,y) \ dA - \iint \limits_R g(x,y) \ dA $$
5. A constant factor can be moved across the double integral sign:
$$ \iint \limits_R kf(x,y) \ dA = k \iint \limits_R f(x,y) \ dA$$
6. If f(x,y) ≤ g(x,y) in a region R, then
$$ \iint \limits_R f(x,y) \ dA \le \iint \limits_R g(x,y) \ dA $$
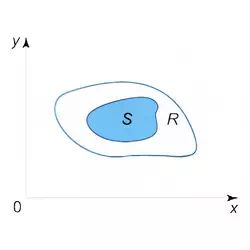
7. If f(x,y) ≥ 0 in a region R and S⊂R, then
$$ \iint \limits_S f(x,y) \ dA \le \iint \limits_R f(x,y) \ dA $$
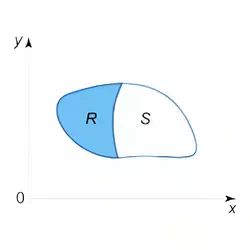
8. If f(x,y) ≥ 0 in a region R and R and S are non-overlapping regions, then
$$ \iint \limits_{R\cup S} f(x,y) \ dA = \iint \limits_R f(x,y) \ dA + \iint \limits_S f(x,y) \ dA $$
Here R∪S is the union of the regions of integration R and S.
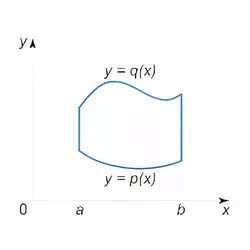
9. Iterated integrals and Fubini’s theorem for a region of type I
style="text-indent:30px;"$$ \iint \limits_R f(x,y) \ dA = \int\limits_a^b \int\limits_{p(x)}^{q(x)} f(x,y) \ dy dx $$
where the region of integration R is defined by the inequalities
R={ (x,y) | a ≤ x ≤ b, p(x) ≤ y ≤ q(x)}.
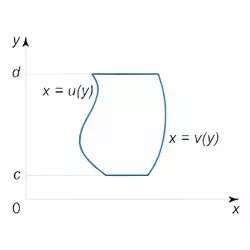
10. Iterated integrals and Fubini’s theorem for a region of type II
$$ \iint \limits_R f(x,y) \ dA = \int\limits_c^d \int\limits_{u(y)}^{v(y)} f(x,y) \ dxdy $$
where the region of integration R is defined by the inequalities
R={ (x,y) | u(y) ≤ x ≤ v(y), c ≤ y ≤ d}.
11. Double integrals over rectangular regions
If R is a rectangular region [a,b]×[c,d], then
$$ \iint \limits_R f(x,y) \ dA = \int\limits_a^b \left( \int\limits_c^d f(x,y) \ dy \right) \ dx = \int\limits_c^d \left( \int\limits_a^b f(x,y) \ dx \right) \ dy $$
In the special case when the integrand f(x,y) can be written as the product g(x)h(y), the double integral is given by
$$ \iint \limits_R f(x,y) \ dxdy = \iint \limits_R g(x)h(y) \ dxdy = \left( \int\limits_a^b g(x)dx \right)\left( \int\limits_c^d h(y)dy \right) $$
12. Change of variables:
$$ \iint \limits_R f(x,y) \ dxdy = \iint \limits_S f[x(u,v),y(u,v)] \left| \frac {\partial (x,y)}{\partial (u,v)} \right| dudv $$
$$ where, \ \left| \frac {\partial (x,y)}{\partial (u,v)} \right| = \left\vert \matrix{ \frac {\partial x}{\partial u} & \frac {\partial x}{\partial v} \cr \frac {\partial y}{\partial u} & \frac {\partial y}{\partial v} } \right\vert \neq 0 $$
This is the jacobian of the transformation (x,y)→(u,v) and S is the pullback of the region R which can be computed by substituting x=x(u,v), y=y(u,v) into the definition of R.
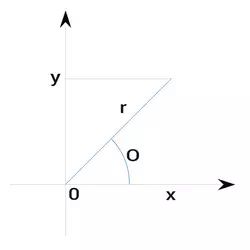
13. Polar coordinates
$$ x=r \cos \theta, y=r \sin \theta $$
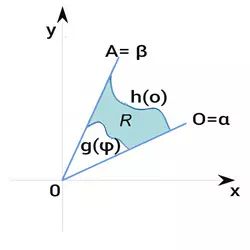
14. Double integrals in polar coordinates
The differential dxdy in polar coordinates is given by the expression
$$ dxdy= \left| \frac {\partial (x,y)}{\partial (r,\theta)}\right| drd\theta = rdrd\theta $$
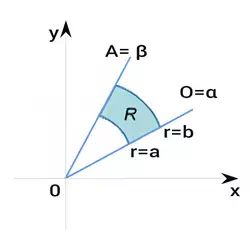
Let the region of integration R be defined as follows:
0 ≤ g(θ) ≤ r ≤ h(θ), α ≤ θ ≤ β,
where β − α ≤ 2π. Then
$$ \iint \limits_R f(x,y) \ dxdy = \int\limits_{\alpha}^{\beta} \int\limits_{g( \theta)}^{h( \theta)} f(r \cos \theta , r \sin \theta) rdrd \theta $$
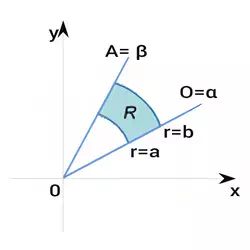
15. Double integral over a polar rectangle
If the region of integration R is a polar rectangle given by the inequalities 0 ≤ a ≤ r ≤ b, α ≤ θ ≤ β, where β − α ≤ 2π, then
$$ \iint \limits_R f(x,y) \ dxdy = \int\limits_{\alpha}^{\beta} \int\limits_a^b f(r \cos \theta , r \sin \theta) rdrd \theta $$
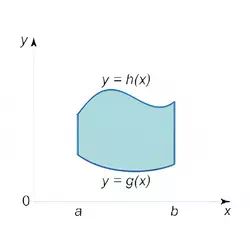
16. Area of a type I region
$$ A= \int\limits_a^b \int\limits_{g(x)}^{h(x)} dydx $$
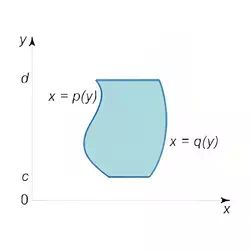
17. Area of a type II region
$$ A= \int\limits_c^d \int\limits_{p(y)}^{q(y)} dxdy $$
18. Volume of a solid
$$ V= \iint \limits_R f(x,y) \ dA $$
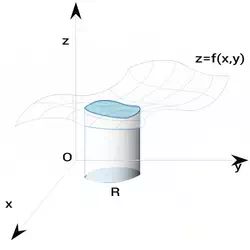
If R is a type I region bounded by x=a, x=b, y=h(x), y=g(x), then
$$ V= \iint \limits_R f(x,y) \ dA = \int\limits_a^b \int\limits_{h(x)}^{g(x)} f(x,y) \ dydx $$
If R is a type II region bounded by y=c, y=d, x=q(y), x=p(y), then
$$ V= \iint \limits_R f(x,y) \ dA = \int\limits_c^d \int\limits_{p(y)}^{q(y)} f(x,y) \ dxdy $$
19. Volume of a solid between two surfaces
If f(x,y) ≥ g(x,y) over a region R, then the volume of the solid between the surfaces z1(x,y) and z2(x,y) over R is given by
$$ V= \iint \limits_R [f(x,y)-g(x,y)] \ dA $$
20. Area and volume in polar coordinates
Let a region S be given in polar coordinates in the xy-plane and bounded by the lines θ = α, θ = β, r = h(θ), r = g(θ). Let also a function f(r,θ) be given in the region S. Then the area of the region S and volume of the solid bounded by the surface f(r,θ) are determined by the formulas
$$ A = \iint \limits_S \ dA = \int\limits_{\alpha}^{\beta} \int\limits_{h(\theta)}^{g(\theta)} rdrd\theta, V= \iint \limits_S f(r,\theta) rdrd\theta $$
21. Surface area:
$$ S= \iint \limits_R \sqrt {1+ \left ( \frac {\partial z}{\partial x} \right)^2 + \left ( \frac {\partial z}{\partial y} \right)^2 } dxdy $$
22. Mass of a lamina
$$ m= \iint \limits_R \rho (x,y) \ dA $$
where the lamina occupies the region R and its density at a point (x,y) is ρ(x,y).
23. Static moments of a lamina
The static moment of a lamina about the x-axis is given by the formula
$$ M_x= \iint \limits_R y \rho (x,y) \ dA $$
Similarly, the static moment of a lamina about the y-axis is expressed in the form
$$ M_y= \iint \limits_R x \rho (x,y) \ dA $$
24. Moments of inertia of a lamina
The moment of inertia about the x-axis is given by
$$ I_x= \iint \limits_R y^2 \rho (x,y) \ dA $$
The moment of inertia about the y-axis is determined by the formula
$$ I_y= \iint \limits_R x^2 \rho (x,y) \ dA $$
The polar moment of inertia is equal to
$$ I_0= \iint \limits_R (x^2+y^2) \rho (x,y) \ dA $$
25. Center of mass of a lamina
$$ \bar x= \frac {M_y}{m} = \frac 1m \iint \limits_R x \rho (x,y) \ dA = \frac {\iint \limits_R x \rho (x,y) \ dA}{\iint \limits_R \rho (x,y) \ dA} $$
$$ \bar y= \frac {M_x}{m} = \frac 1m \iint \limits_R y \rho (x,y) \ dA = \frac {\iint \limits_R y \rho (x,y) \ dA}{\iint \limits_R \rho (x,y) \ dA} $$
26. Charge of a plate
$$ Q= \iint \limits_R \sigma (x,y) \ dA $$
where the electrical charge is distributed over the region R and its density at a point (x,y) is σ(x,y).
27. Average of a function
$$ \mu = \frac 1S \iint \limits_R f(x,y) \ dA ,$$
$$ where, \ S= \iint \limits_R \ dA $$


