Definite Integration

Integrands: f, g, u, v

Antiderivatives: F, G

Independent variables: x, t

Limits of integration: a, b, c, d

Subintervals of integration: Δx_i

Arbitrary point of a subinterval: ξi

Natural numbers: n, i

Area of a curvilinear trapezoid: S

1. The definite integral of the function f(x) over the interval [a,b] is defined as the limit of the integral sum (Riemann sums) as the maximum length of the subintervals approaches zero.

$$ \int\limits_a^b f(x)dx= \lim_{\substack{ n \to \infty \\ \text{max} \ \Delta {x_i} \to 0 }} \sum_{i=1}^n f( \xi_i) \Delta x_i, $$

$$ where \ \Delta x_i=x_i-x_{i-1}, x_{i-1} \le \xi_i \le x_i. $$

2. The definite integral of 1 is equal to the length of the interval of integration:

$$ \int\limits_a^b 1 dx= b-a $$

3. A constant factor can be moved across the integral sign:

$$ \int\limits_a^b kf(x)dx= k \int\limits_a^b f(x)dx $$

4. The definite integral of the sum of two functions is equal to the sum of the integrals of these functions:

$$ \int\limits_a^b [f(x)+g(x)]dx= \int\limits_a^b f(x)dx + \int\limits_a^b g(x)dx $$

5. The definite integral of the difference of two functions is equal to the difference of the integrals of these functions:

$$ \int\limits_a^b [f(x)-g(x)]dx= \int\limits_a^b f(x)dx - \int\limits_a^b g(x)dx $$

6. If the upper and lower limits of a definite integral are the same, the integral is zero:

$$ \int\limits_a^b f(x)dx = 0 $$

7. Reversing the limits of integration changes the sign of the definite integral:

$$ \int\limits_a^b f(x)dx = -\int\limits_b^a f(x)dx $$

8. Suppose that a point c belongs to the interval [a,b]. Then the definite integral of a function f(x) over the interval [a,b] is equal to the sum of the integrals over the intervals [a,c] and [c,b]:

$$ \int\limits_a^b f(x)dx= \int\limits_a^c f(x)dx + \int\limits_c^b f(x)dx $$

9. The definite integral of a non-negative function is always greater than or equal to zero:

$$ \int\limits_a^b f(x)dx \ge 0 \ if \ f(x) \ge 0 \ in \ [a,b] $$

10. The definite integral of a non-positive function is always less than or equal to zero:

$$ \int\limits_a^b f(x)dx \le 0 \ if \ f(x) \le 0 \ in \ [a,b] $$

11. Fundamental theorem of calculus

$$ \int\limits_a^b f(x)dx = F(x) |_a^b = F(b)-F(a), if \ F'(x)=f(x) $$

12. Substitution rule for definite integrals

$$ if \ x=g(t) \ then $$

$$ \int\limits_a^b f(x)dx = \int\limits_c^d f(g(t))g'(t)dt $$

$$ where, \ c=g^{-1}(a), d=g^{-1}(b) $$

13. Integration by parts for definite integrals

$$ \int\limits_a^b udv= (uv)|_a^b - \int\limits_a^b vdu $$

14. Trapezoidal approximation of a definite integral

$$ \int\limits_a^b f(x)dx = \frac {b-a}{2n} \left[ f(x_0) + f(x_n) + 2 \sum_{i=1}^{n-1} f(x_i) \right] $$

15. Approximation of a definite integral using Simpson’s rule

$$ \int\limits_a^b f(x)dx = \frac {b-a}{3n} \left[ f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \cdots + 4f(x_{n-1}) + f(x_n) \right], $$

$$ where \ x_i=a+ \frac {b-a}{n}i, i=0,1,2,\cdots ,n $$

16. Area under a curve

$$ S= \int\limits_a^b f(x)dx = F(b)-F(a), $$

$$ where, \ F'(x)=f(x) $$

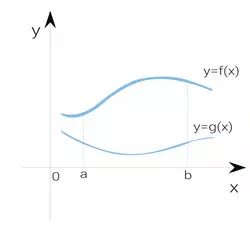
17. Area between two curves

$$ S= \int\limits_a^b [f(x) -g(x)]dx = F(b)-G(b)-F(a)+G(a) $$

$$ where, \ F'(x)=f(x), \ G'(x)=g(x) $$